가장 먼 두 점의 거리를 구할때 사용되어지는 알고리즘인 로테이팅 캘리퍼스(회전하는 캘리퍼스)에 대해서 소개하려고 한다. 수학을 좋아하고 잘하는 사람들은 수학에서 이미 접해봤을 수도 있는 내용이다.
로테이팅 캘리퍼스란?
rotating + callipers의 합성어로 rotating은 돌아가는, 회전하는이란 뜻이고, callipas는 길이를 재는 도구이다. 즉, 놓여있는 점들 중 가장 먼 두 점의 거리를 구할때 돌면서 구하겠다는 뜻이다. two pointer기반으로 이루어지며 몇가지 수학적 사실들을 기반으로 이루어지게 된다.
진행 방식
일단 점들중 가장 거리가 먼 두 점이 있다면 그 두 점은 모두 볼록 껍질 위에 있다라는 사실을 전제로 한다. 완벽히 증명은 되지 않아도 어느정도 직관적으로 이해할 수 있는 사실이다. 따라서 전체 점에서 볼록껍질을 잡고 시작한다.
볼록껍질에서 가장 먼 두 점 사이의 거리를 구하는 방법은 다음과 같이 이루어진다.
1. 1번점을 A, 2번점을 C라고 하자.
2. A의 다음 점을 B, C의 다음 점을 D라고 하자.
3. A와 C의 거리를 잰다.
4. 벡터 AB와 벡터 CD의 CCW를 이용해 두 벡터가 정반대에 가까워지도록 A를 한칸 돌리거나 C를 한칸 돌린다.
5. A가 처음으로 올때까지 반복한다.
그림으로 표현하면 다음과 같이 진행된다.


왼쪽과 같이 점들이 있을때 그라함 알고리즘을 이용하여 컨벡스 헐을 잡을 수 있다.


왼쪽 그림처럼 컨벡스 헐에 포함되는 점들만 남기고, 오른쪽 그림처럼 1,2 번과정을 진행한다.


이 후 진행하면서 (AB)-(CD) CCW가 반시계면 C를 한 칸 움직이고, 시계면 A를 한칸 움직인다.

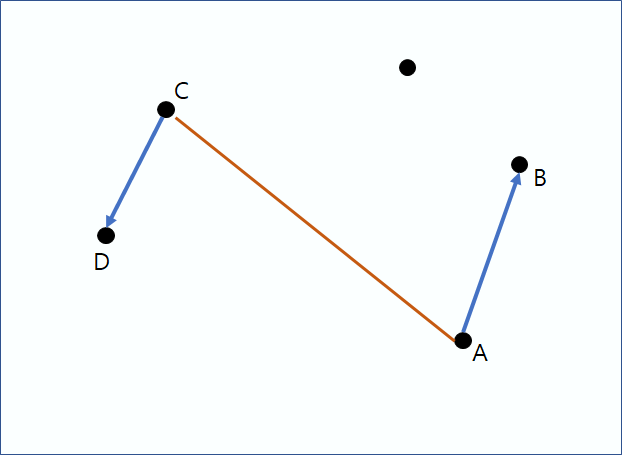
계속 움직이면서 노란색의 길이 즉, A와 C의 거리의 최댓값을 계속 업데이트 해준다.
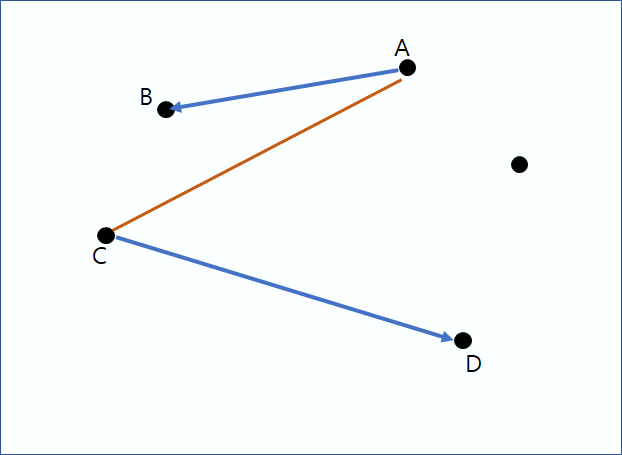
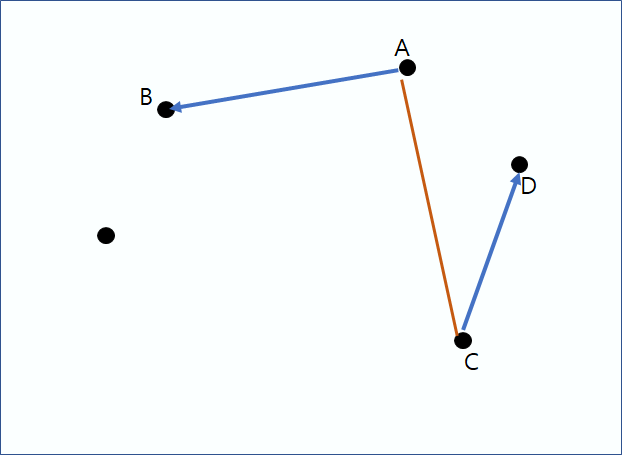
중간과정 생략
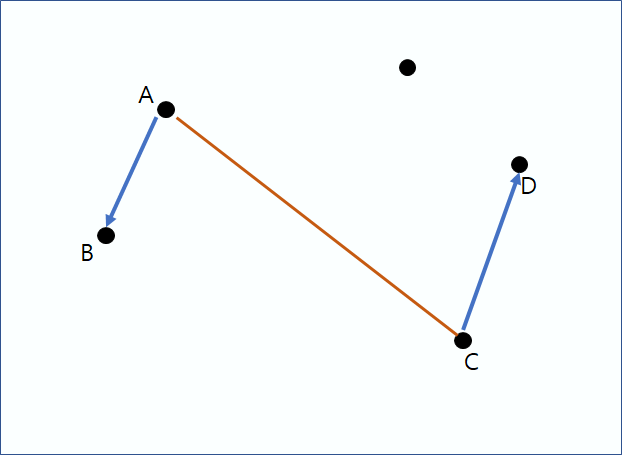
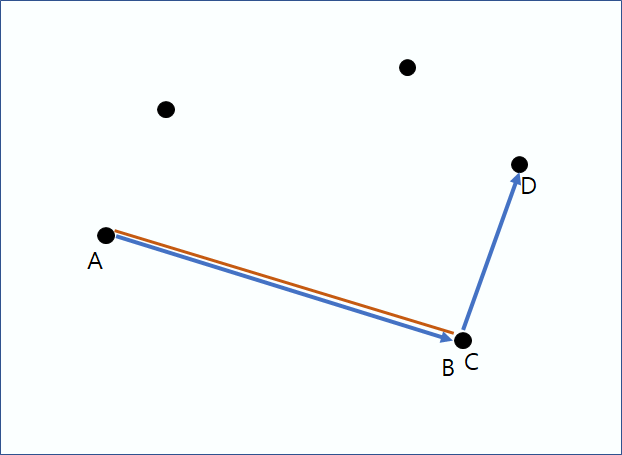
계속 진행하다가 A가 맨 처음 지점으로 돌아올 때 까지 반복한다.
증명
알고리즘의 증명이 궁금하다면 https://stonejjun.tistory.com/140 로.
코드
이 코드는 문제 https://www.acmicpc.net/problem/10254의 코드이다.
위의 방법을 A를 한 칸 움직일때 마다 C를 최대 어디까지 움직일 수 있는 지를 확인하여 구하는 코드이다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
|
#include<bits/stdc++.h>
using namespace std;
typedef long long int ll;
struct poi{
ll x,y;
};
ll ccw(poi a,poi m,poi b)
{
ll t=(a.x-m.x)*(b.y-m.y)-(a.y-m.y)*(b.x-m.x);
return (t<0)-(t>0);
}
ll cccw(poi a,poi b,poi c,poi d){
d.x-=(c.x-b.x);
d.y-=(c.y-b.y);
//printf("%lld %lld %lld %lld %lld %lld %lld\n",a.x,a.y,b.x,b.y,d.x,d.y,ccw(a,b,d));
return ccw(a,b,d);
}
ll dist(poi a,poi b)
{
return (b.x-a.x)*(b.x-a.x)+(b.y-a.y)*(b.y-a.y);
}
poi arr[1010101];
bool sf(poi a,poi b){
if(a.x!=b.x) return a.x<b.x;
return a.y<b.y;
}
bool sf2(poi a,poi b){
return (ccw(arr[1],a,b)>0||(ccw(arr[1],a,b)==0&&dist(arr[1],a)<dist(arr[1],b)));
}
poi ch[1010101];
ll far[1010101];
int main(){
ll t;
scanf("%lld",&t);
while(t--){
ll i,j,k,l,m,n;
scanf("%lld",&n);
for(i=1;i<=n;i++)
scanf("%lld %lld",&arr[i].x,&arr[i].y);
sort(arr+1,arr+1+n,sf);
sort(arr+2,arr+1+n,sf2);
ch[0]=arr[1];
ch[1]=arr[2];
ll fl=2;
ll cnt=2;
for(i=3;i<=n;i++){
while(fl>=2&&ccw(ch[fl-2],ch[fl-1],arr[i])<=0)
fl--;
ch[fl]=arr[i];
fl++;
}
ll fl2=1;
ll ans=0;
poi ans1,ans2;
for(i=0;i<fl;i++){
while((fl2+1)!=i&&cccw(ch[i],ch[i+1],ch[fl2%fl],ch[(fl2+1)%fl])>0){
if(ans<dist(ch[i],ch[fl2%fl])){
ans1=ch[i];
ans2=ch[fl2%fl];
ans=dist(ch[i],ch[fl2%fl]);
}
fl2++;
}
//printf("%lld %lld\n",i,fl2);
if(ans<dist(ch[i],ch[fl2%fl])){
ans1=ch[i];
ans2=ch[fl2%fl];
ans=dist(ch[i],ch[fl2%fl]);
}
}
printf("%lld %lld %lld %lld\n",ans1.x,ans1.y,ans2.x,ans2.y);
}
}
Colored by Color Scripter
|
'코딩 > 알고리즘 & 자료구조' 카테고리의 다른 글
| Techniques In DP (1) - bitmask (0) | 2020.03.25 |
|---|---|
| 이분 매칭(Bipartite Matching) (3) | 2020.03.20 |
| Geometry (3) - 컨벡스 헐 잡기 (그라함 알고리즘) (0) | 2020.03.08 |
| Geometry (2) - 내부 판별 (0) | 2020.03.08 |
| Geometry (1) - CCW & 교차 판별 (0) | 2020.03.07 |