이 글을 쓰게 된 동기는 굉장히 재미있다. 증명을 원하시는 분이 있었고 누군가가 내 글을 링크해주신 것을 알게 되었지만 그 글에서는 증명이 없었고, 그래서 관심을 가지게 되었다. 어느 정도 생각해본 결과 대충 증명이 된 것 같아서 일단은 빠르게 글을 써보려고 한다.
따라서 증명이 완벽하지 않을 수도 있으며 뇌피셜일 수도, 많이 생략했을 수도 있다. 하지만 오히려 직관적으로 받아들여질 수도 있다. 댓글로 비판과 지적은 언제나 환영한다.
이 글을 읽기 전에...
로테이팅 캘리퍼스 설명글 stonejjun.tistory.com/42
본인은 설명을 굉장히 못하기 때문에 어쩔 수 없이 설명하려면 코드와 함께 설명하는 수밖에 없을 것 같다. 위 글의 맨 마지막에 코드가 있고, 증명과정에서 그 코드를 언급을 하게 될 것 같다.
이 글은 이미 볼록껍질에서를 기준으로 생각한다.
이 글에서 방향성 (다음, 이전)은 볼록 껍질에서 반시계 방향으로 다음, 이전점을 말한다.
증명
볼록껍질에서 가장 먼 두 점을 고르자. 그 두 점을 A와 B라고 명명한다. 이제 우리는 하던 대로 로테이팅 캘리퍼스 과정에서 두 점의 거리를 지속적으로 잴 것인데, 그 두 점 중에 A와 B를 재는 경우가 포함되는지를 확인하면 된다.
A가 i가 되었다고 하자. 이때 fl2가 더해지는 과정에서 한 번이라도 fl2==B가 되면 되는 것이다. 문제가 되는 경우는
1. 시작부터 fl2가 B 뒤에 있어서 같아질 수 없는 경우
2. fl2가 B에 도달하기 전에 끝나는 경우
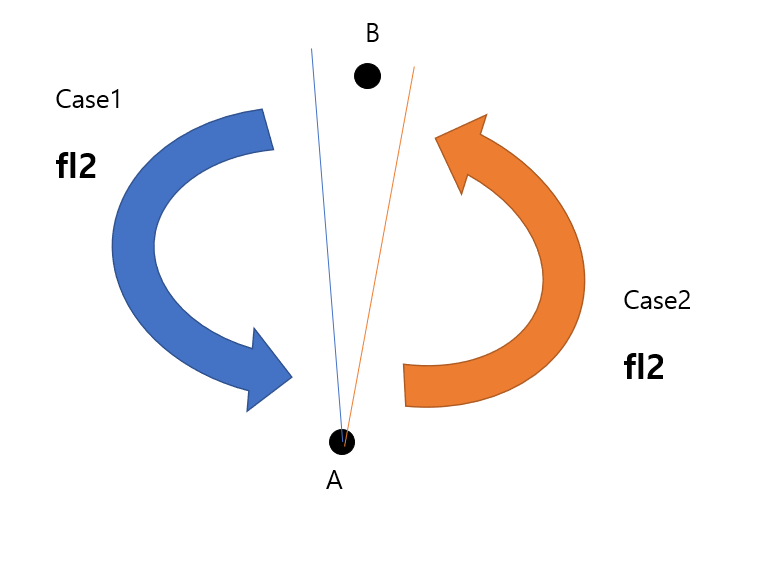


위의 그림에서 Case 1이 B 이후부터 fl2를 탐색하기 시작하여 fl2를 만나지 못하는 것이고, Case2가 fl2가 B까지 가지 않기 때문에 만나지 못하는 상황이다.
우리의 목표는 바뀌었다. 이제는 저 두 가지 경우가 일어나지 않는다는 것만 증명하면, 무조건 A와 B사이의 거리를 잴 수밖에 없고, 따라서 로테이팅 캘리퍼스의 정당성이 증명된다.
Case 1 - 불가능의 증명
Case 1을 살펴보자. A에 가기 이전에 이미 fl2가 B를 지나쳤다는 것은 A와 B사이에 어떠한 점 C가 존재해서 B에서 다음점으로 fl2를 넘겼다는 것이다. B의 다음 점을 D라고 해보자. 또한 C의 다음 점을 C'이라고 할 것이다. 그러면 아래와 같은 그림이 나오게 된다.

C가 현재 i의 역할을 하고 있으며 fl2가 B에서 D로 넘어가게 되는 것이다. fl2가 B에서 D로 넘어갔다는 것은 반직선 C->C'과 반직선 B->D가 이루는 CCW가 양수(반시계 방향)라는 것이고 위의 그림은 틀렸다.

다음과 같은 그림이 좀 더 정확하며 이와 같은 위치 관계가 나오게 될 것이다. 그런데 위에서 언급한 모든 점들은 볼록 껍질을 이루고 있기 때문에 기울기 관계에 의해서 (C->C', B->D)의 CCW 값이 양수이면 (C->A, B->D)의 CCW 값이 양수가 된다.
이는 선분 AB에 수직하고 A, B를 지나는 직선을 그렸을 때 C와 D 둘 중 하나는 직선 밖에 있게 되며, 따라서 AD나 BC 중 하나는 AB보다 거리가 멀게 된다.


즉 다시 말하여, (C->A,B->D)의 CCW값이 양수이다. 이를 만족하기 위해서는 왼쪽 그림처럼 D가 두 직선 밖에 있거나, 오른쪽 그림처럼 C가 두 직선 밖에 있어야 하는데, 왼쪽의 경우 AD>AB가 되며, 오른쪽의 경우 BC>AB가 되어 둘 다 AB의 거리가 가장 멀다는 처음 가정에 모순이다.
따라서 Case 1의 경우는 일어나지 않는다!
Case 2 - 불가능의 증명
이번에는 A의 다음점 A'과 B의 전 점 B'을 잡아보자. fl2가 B까지 도달하지 못했다는 것은 그 이전에 CCW값이 음수가 되었다는 것이다. 이번에도 잘 생각해보면 볼록 껍질이기 때문에 위와 같이 이전에 음수가 되었으면 (A->A', B'->B)의 CCW값은 당연히 음수가 된다.

여기서부터는 굉장히 익숙하다. Case 1을 잘 따라왔으면 이미 눈에 보였을 수도 있다. (A->A', B'->B)의 CCW 값이 음수이기 때문에 AB'의 거리가 AB의 거리보다 크거나 A'B의 거리가 AB의 거리보다 크게 된다. 이는 맨 처음에 가정하였던 AB사이의 거리가 가장 멀다에 모순이 된다.
따라서 Case2의 경우도 일어나지 않는다!
종합
로테이팅 켈리퍼스를 했다고 하자. i가 가장 먼 두 점 중한 점 일 때, fl2가 나머지 한 점이 되는 경우가 있는지를 생각해야 한다. 가장 먼 두 점 중 나머지 한 점이 fl2가 되지 않는 경우는 절대 일어나지 않음을 증명하였다. 따라서 fl2는 무조건 한 번은 나머지 한 점이 될 수밖에 없고, 그 순간의 거리 또한 측정하기 때문에 로테이팅 캘리퍼스에서는 가장 먼 두 점 사이의 거리를 항상 특정할 수 있다.
이모저모
이걸 생각하다가 왜 꼭 CCW여야 하는지, 거리로 나타내면 안 되는지를 생각해서 코딩을 해봤는데 틀렸다. 어떤 한 점에 대해서 나머지 점들의 거리에 대한 함수가 위로 볼록 형태로 나올 줄 알았는데 그러지 않더라...

지금 물론 좌우반전이 되었지만, 아무튼 오히려 가운데 있는 점이 제일 거리가 가깝다. 그래서 더 이상 투 포인터를 진행하지 않고 중간에서 끊어버린다. 따라서 CCW가 아니라 거리로 비교를 하면 가장 먼 두 점 사이의 거리를 잴 수 없다.
'코딩 > 알고리즘 & 자료구조' 카테고리의 다른 글
| Segment Tree 심화 (6) - Persistent Segment Tree (0) | 2020.11.12 |
|---|---|
| Segment Tree 심화 (5) - HLD (Heavy-Light Decomposition) (2) | 2020.09.10 |
| 내가 사용하는 STL (6) - lower_bound & upper_bound & 좌표압축 (0) | 2020.08.26 |
| 내가 사용하는 STL (4) - 덱 (Deque) (0) | 2020.08.06 |
| 내가 사용하는 STL (5) - 우선 순위 큐 (priority queue) (0) | 2020.08.04 |