이번에 소개할 내용은 Persistent Segment Tree이다. Segment Tree 의 한 종류로 굉장히 특별한 부분을 맡고 있다.
Persistent Segment Tree의 사용
이 문제를 보자. www.acmicpc.net/problem/16978
물론 오프라인이기 때문에 쓸 수 있는 테크닉으로 풀 수도 있지만, 이 문제가 주어진 쿼리를 순서대로 대답해야하는 온라인 문제라고 생각을 해보자.
일단은 세그먼트 트리를 사용할 것이다. 그런데 우리는 임의의 k에 대해서 k번째 쿼리까지만 의해서만 바뀐 그 시점의 세그먼트 트리를 알고 싶다.
가장 직관적인 방법은 모든 k에 대한 세그트리의 상황을 저장해 놓는 것이다. 하지만 O(QN)의 시간과 공간 복잡도가 필요할 것이고, 당연히 Q와 N은 100000이 넘을 것이다. 이런 상황에서 사용하게 되는 것이 PST. 즉, persistent segment tree이다.
PST의 작동 방식
따라서 우리는 모든 세그먼트 트리를 다 들고 있지 않을 것이다. 우리는 세그먼트 트리에서 업데이트 할 때도, 모든 노드를 다 하지 않는다. 특정 위치를 업데이트 할 때, 그 위치를 포함하고 있는 구간에 해당하는 노드들만 업데이트 한다.
이와 같은 방식으로 업데이트 하는 위치를 포함하는 노드들만 새로 만들어서 저장을 하고 있는 것이다.
따라서 한 쿼리에 대해서 한 위치의 값만 변화될 때 PST를 사용하기 편하다.
예를 들어서 4개의 원소 중 세번째 원소를 업데이트 하려고 한다. (세그먼트 트리에서는 6번 노드) 그러면 나이브한 방법으로는 아래의 사진과 같이 두 개의 독립적인 세그먼트 트리가 생긴다.
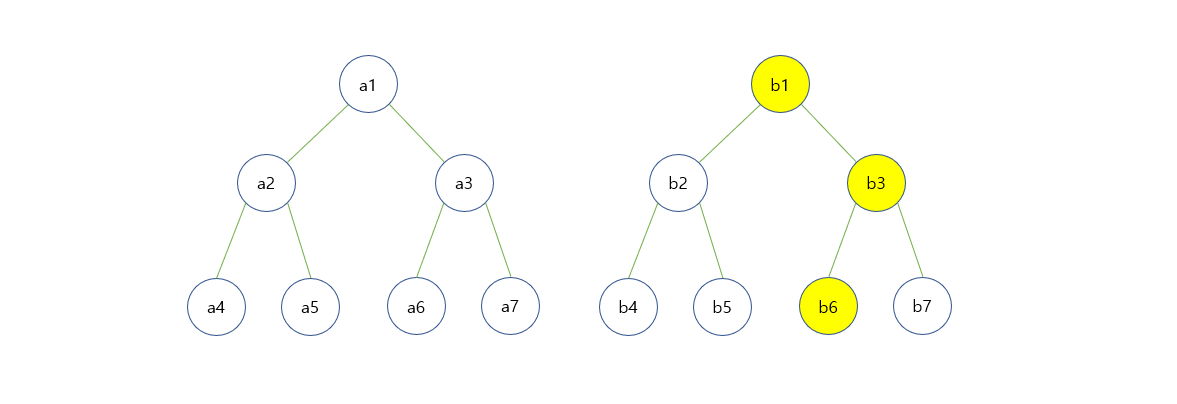
하지만, persistent segment tree는 세그먼트 트리 노드를 재활용한다. 이는 아래의 그림과 같이 작동한다.
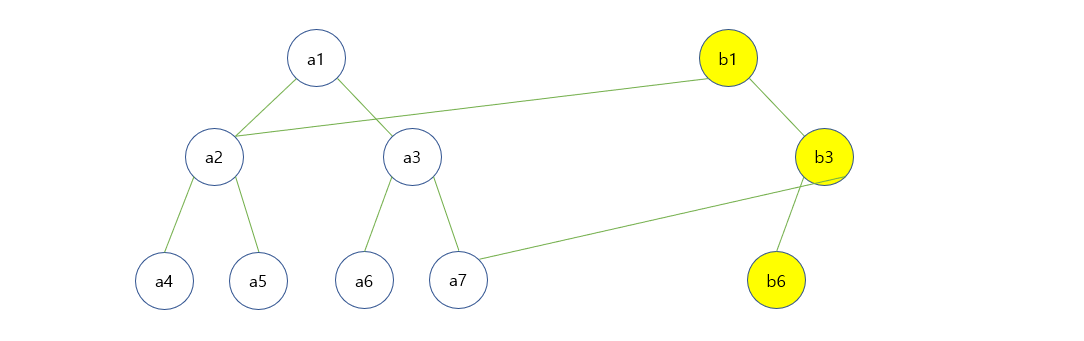
b2를 새로만드는 대신 a2를 자식으로써 연결해준다. 이와 같이 b1,a2,b3,a4,a5,b6,a7오 이루어진 2번째 세그먼트 트리가 완성되었다. 이렇게 업데이트 하는 부분만 들고 있으면, 한 개의 세그먼트 트리를 만드는데도 logN, 공간의 크기도 logN만 사용하게 된다.
구현 방식
기본적으로 동적 세그먼트 트리를 짜게 된다. 동적 세그트리를 짜는 방법은 크게 두 가지로, 포인터를 이용하는 방법과 인덱스를 이용하는 방법이 있다. 처음에 포인터로 구현을 하려다가 너무 복잡하고 신경쓸 것이 많아서(사람이 할게 못되서) 인덱스를 이용한 구현 방식으로 바꾸었다. 나름 세심하게 신경써야할 디테일이 많다.
코드
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 | struct node{ ll l,r,val; }; vector<node> tree; void mak(){ tree.pb({-1,-1,0}); } void init(ll s,ll e,ll nod){ if(s==e) return; mak(); tree[nod].l=tree.size()-1; mak(); tree[nod].r=tree.size()-1; init(s,(s+e)/2,tree[nod].l); init((s+e)/2+1,e,tree[nod].r); } void upt(ll idx,ll val,ll s,ll e,ll nod1,ll nod2){ if(idx<s||idx>e){ tree[nod2].l=tree[nod1].l; tree[nod2].r=tree[nod1].r; tree[nod2].val=tree[nod1].val; return; } tree[nod2].val=tree[nod1].val+val; if(s==e) return; if(idx<=(s+e)/2){ tree[nod2].r=tree[nod1].r; mak(); tree[nod2].l=tree.size()-1; upt(idx,val,s,(s+e)/2,tree[nod1].l,tree[nod2].l); } else{ tree[nod2].l=tree[nod1].l; mak(); tree[nod2].r=tree.size()-1; upt(idx,val,(s+e)/2+1,e,tree[nod1].r,tree[nod2].r); } } ll sol(ll l,ll r,ll s,ll e,ll nod){ if(e<l||r<s) return 0; if(l<=s&&e<=r) return tree[nod].val; return sol(l,r,s,(s+e)/2,tree[nod].l)+sol(l,r,(s+e)/2+1,e,tree[nod].r); } | cs |
'코딩 > 알고리즘 & 자료구조' 카테고리의 다른 글
| Offline dynamic Connectivity (0) | 2021.04.08 |
|---|---|
| Segment Tree 심화 (5) - HLD (Heavy-Light Decomposition) (2) | 2020.09.10 |
| 로테이팅 캘리퍼스의 증명 (2) | 2020.09.02 |
| 내가 사용하는 STL (6) - lower_bound & upper_bound & 좌표압축 (0) | 2020.08.26 |
| 내가 사용하는 STL (4) - 덱 (Deque) (0) | 2020.08.06 |