'트리는 센트로이드, 그래프는 SCC를 잡고 보면 편해진다' 라는 말이 있듯이 '기하는 컨벡스 헐을 잡고 보면 편해진다' 라는 말이 있다. 그 만큼 컨벡스 헐은 기하 문제에서 굉장히 중요한 역할을 한다. 이번 글에서는 무작위 점들에서 컨벡스 헐을 잡는 대표적인 방법인 그라함 알고리즘을 소개하려고 한다.
컨벡스 헐(Convex Hull)이란?
한국어로는 볼록 껍질이고, 볼록 껍질이란 말이 이 단어의 의미를 정말 잘 설명해 준다고 생각한다. 말 그대로 '볼록' 한 '껍질'이다. 점들이 막 주어져 있을때 모든 점을 포함하는 볼록한 다각형을 의미한다. 그리고 보통 그 다각형의 꼭짓점을 모두 구하는 것을 '컨벡스 헐을 잡는다'라고 이야기 한다.

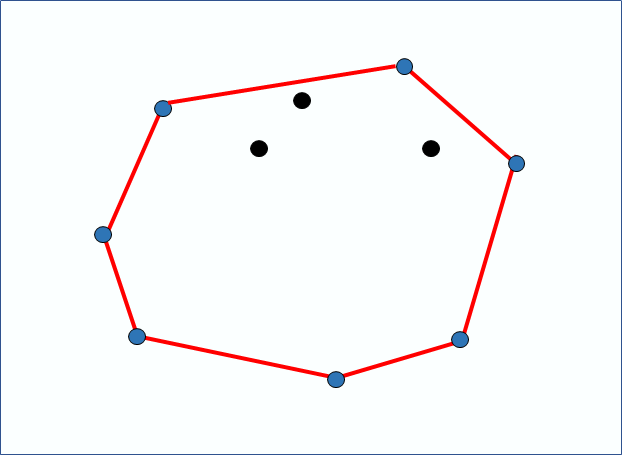
왼쪽 그림과 같이 점 들이 놓여져 있을때 오른쪽의 빨간 직선으로 이루어진 도형을 컨벡스 헐이라 하고, 우리의 목표는 저 파란색으로 칠한 점들만 골라 내는 것이다.
이때도 역시 CCW를 이용한다. 컨벡스 헐에서 연속한 세 점을 한 쪽 방향으로 잡으면 모든 결과가 같다는 것을 알 수 있고, 이를 이용한다.
Graham Algorithm
컨벡스 헐을 잡는 대표적인 알고리즘인 그라함 알고리즘은 점 들을 정렬하는데에서 시작한다.
1. 컨벡스 헐에 무조건 들어가는 점 하나를 잡는다. (보통 가장 x좌표가, y좌표가 작은 점)
2. 그 점을 기준으로 기울기 순으로 정렬한다. 같은 기울기면 거리 순으로 정렬.
3. 점들을 그룹에 순서대로 넣는다.
4. 넣으면서 그룹의 제일 최근 3점의 ccw가 옳지 않으면 그 세 점중 중간 점을 뺀다.
5. 3~4를 반복하면서 1번점까지 돌아온다.
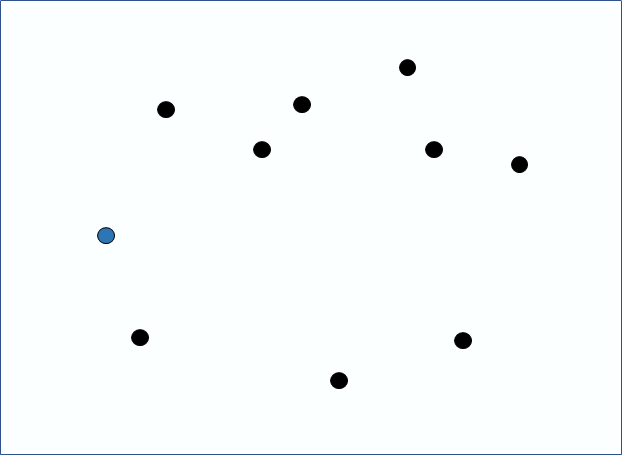
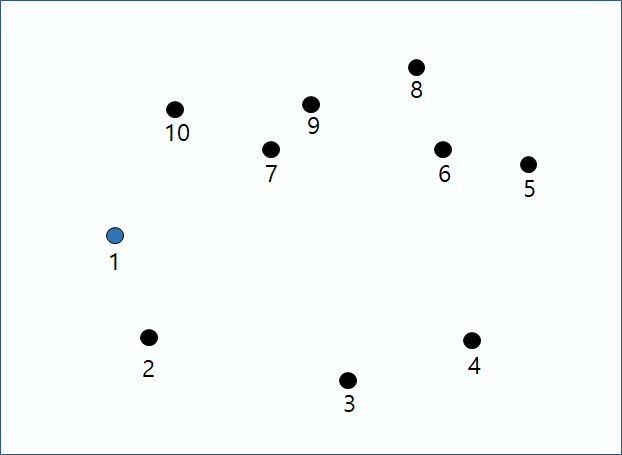
왼쪽과 같이 파란 점 하나를 잡는 것이 1번 과정, 오른쪽과 같이 기울기에 따라 정렬된 것이 2번 과정이다.
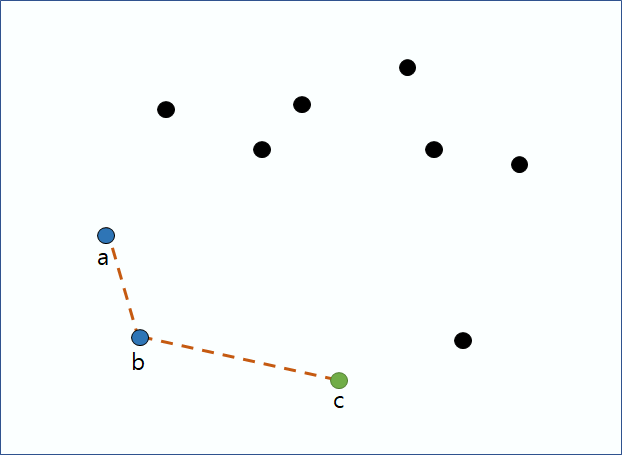

1번점부터 순서대로 넣으면서 제일 최근 3개의 점을 확인한다. 다 반시계이기 때문에 계속 넣으면서 진행한다.


왼쪽 그림 즉, 7번 점을 넣을때 까지는 문제가 없지만, 오른쪽 그림에서 8번점을 넣을때 가장 최근 3개의 점이 시계방향을 이루는 것을 확인했다. 따라서 B에 해당하는 7번점을 제외한다.

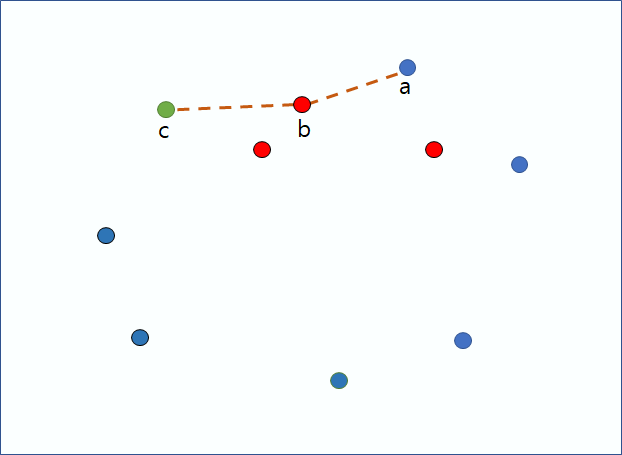
이 과정은 반시계 방향이 나올때까지 계속한다. 왼쪽 그림처럼 7번 점에 이어서 6번점도 빼준다. 나머지도 이와 같은 과정으로 계속 진행해준다.

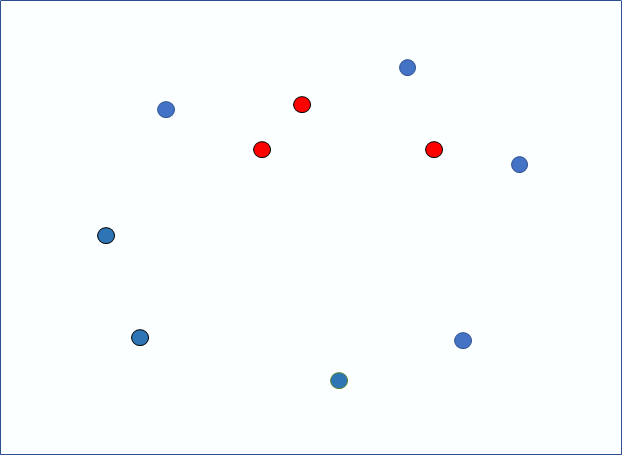
왼쪽 그림처럼 1번점에 다시 도달했다면 마지막으로 확인하고 종료한다.
결과는 오른쪽 그림과 같이 나왔고, 정확히 우리가 원했던 파란 점들을 얻을 수 있었다.
코드
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
|
#include<bits/stdc++.h>
using namespace std;
typedef long long int ll;
struct poi{
ll x,y;
};
ll ccw(poi a,poi m,poi b)
{
ll t=(a.x-m.x)*(b.y-m.y)-(a.y-m.y)*(b.x-m.x);
return (t<0)-(t>0);
}
ll dist(poi a,poi b)
{
return (b.x-a.x)*(b.x-a.x)+(b.y-a.y)*(b.y-a.y);
}
poi arr[1010101];
bool sf(poi a,poi b){
if(a.x!=b.x)return a.x<b.x;
return a.y<b.y;
}
bool sf2(poi a,poi b){
return (ccw(arr[1],a,b)>0||(ccw(arr[1],a,b)==0&&dist(arr[1],a)<dist(arr[1],b)));
}
poi ch[1010101];
int main(){
ll i,j,k,l,m,n;
scanf("%lld %lld",&n,&m);
for(i=1;i<=n;i++)
scanf("%lld %lld",&arr[i].x,&arr[i].y);
sort(arr+1,arr+1+n,sf);
sort(arr+2,arr+1+n,sf2);
ch[0]=arr[1];
ch[1]=arr[2];
ll fl=2;
for(i=3;i<=n;i++){
while(fl>=2&&ccw(ch[fl-2],ch[fl-1],arr[i])<=0)
fl--;
ch[fl]=arr[i];
fl++;
}
}
Colored by Color Scripter
|
'코딩 > 알고리즘 & 자료구조' 카테고리의 다른 글
| 이분 매칭(Bipartite Matching) (3) | 2020.03.20 |
|---|---|
| Geometry (4) - 로테이팅 캘리퍼스 (10) | 2020.03.13 |
| Geometry (2) - 내부 판별 (0) | 2020.03.08 |
| Geometry (1) - CCW & 교차 판별 (0) | 2020.03.07 |
| Segment Tree With Lazy Propagtion (0) | 2020.02.29 |