이번 글에서는 어떤 점이 도형의 내부에 있는지 판별하는 알고리즘을 설명하려고 한다. 엄청 많이 쓰이는 것도, 엄청 까다로운 것도 아니지만 나름 중요하며, 어쩌면 쉬어가는 타임으로 받아들일 수도 있다.
도형에서의 점의 내부 판별
들어본 사람은 들어봤을만한 문제이다. 꼭 정보가 아니어도 한 번쯤은 책이나 어디에선가 점이 도형의 내부에 있는지 외부에 있는지에 대해서 설명한 것을 봤을만하다. 점에서 외부로 선을 그었을 때 도형과 짝수번 만나면 외부, 홀수번 만나면 내부이다.
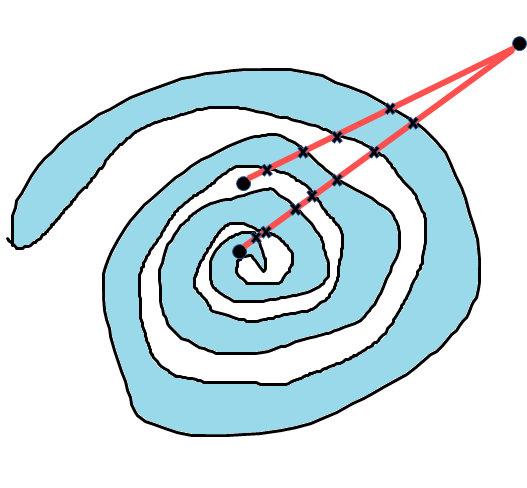
위의 그림에서 확인하고 싶은 점에 대해서 먼 점을 찍으면 그 둘을 이은 선분이 도형을 한 번 지나칠때 마다 내부와 외부가 바뀐다는 사실을 알 수 있다. 따라서 전 글에 나와있는 선분 교차 알고리즘을 이용하면 쉽게 문제를 해결할 수 있다.
이 때 두 점을 이은 선분이 도형의 꼭짓점을 지나치면 한 번 카운팅 해야하는데 두 번이 될 수 있다. 따라서 먼 점을 잡을 때 기존점(x,y)에서 기울기가 굉장히 작은 직선을 잡으면 된다. (x+1e9,y+1) 그러면 절대로 꼭짓점에서 만나지 않는다.
BOJ 1688
가장 간단하고 대표적인, 점이 내부에 있는지 외부에 있는지 판별하는 문제이다. 이때 경계면 내부로 치기 때문에 점이 선의 경계에 있는지도 같이 확인을 해주어야 한다.
코드
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
|
#include<bits/stdc++.h>
using namespace std;
typedef long long int ll;
struct poi{
ll x,y;
bool operator <(const poi &t) const {
if(x==t.x) return y<t.y;
return x<t.x;
}
};
struct lin{
poi f,s;
};
ll ccw(poi a,poi m,poi b)
{
ll t=(a.x-m.x)*(b.y-m.y)-(a.y-m.y)*(b.x-m.x);
return (t<0)-(t>0);
}
bool cross(lin a,lin b)
{
if(ccw(a.f,a.s,b.f)*ccw(a.f,a.s,b.s)==0&&ccw(b.f,b.s,a.f)*ccw(b.f,b.s,a.s)==0)
return !(max(a.f, a.s)<min(b.f,b.s)||max(b.f, b.s)<min(a.f,a.s));
return ccw(a.f,a.s,b.f)*ccw(a.f,a.s,b.s)<=0&&ccw(b.f,b.s, a.f)*ccw(b.f,b.s,a.s)<=0;
}
bool online(lin a,poi b){
if(ccw(a.f,b,a.s)==0&&((a.f.x<=b.x&&b.x<=a.s.x&&a.f.y<=b.y&&b.y<=a.s.y)||(a.f.x>=b.x&&b.x>=a.s.x&&a.f.y>=b.y&&b.y>=a.s.y)))
return true;
return false;
}
poi arr[1010101];
lin li[1010101];
int main(){
ll i,j,k,l,m,n;
scanf("%lld",&n);
for(i=1;i<=n;i++)
scanf("%lld %lld",&arr[i].x,&arr[i].y);
arr[n+1]=arr[1];
for(i=1;i<=n;i++)
li[i]={arr[i],arr[i+1]};
for(i=1;i<=3;i++){
poi p1,p2;
ll cnt=0;
scanf("%lld %lld",&p1.x,&p1.y);
p2.x=p1.x+1e9;
p2.y=p1.y+1;
lin l1={p1,p2};
for(j=1;j<=n;j++){
if(cross(l1,li[j])) cnt++;
if(online(li[j],p1)){
cnt=1;
break;
}
}
printf("%lld\n",cnt%2);
}
}
|
볼록다각형에서의 내부 판별
임의의 도형에 대해서는 어떤 점의 내부성 판별을 위해 드는 시간복잡도가 O(N)이다. 하지만 볼록다각형이라면 O(logN)만에 하나의 점을 판별할 수 있다.
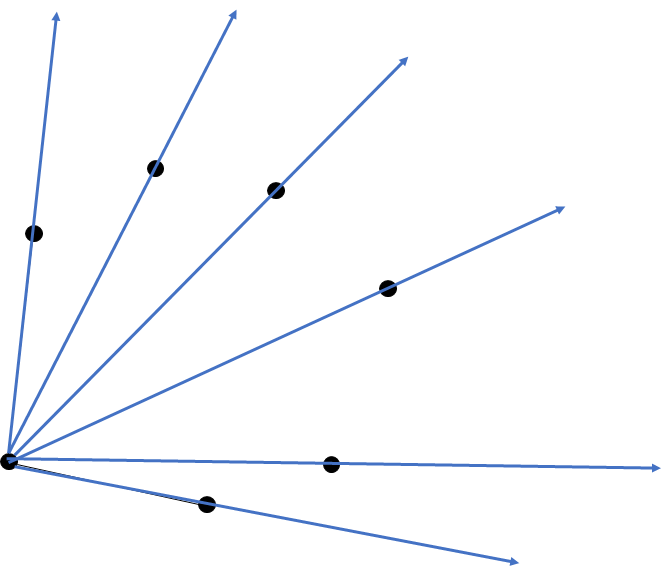
위와 같이 볼록다각형을 이루는 경우에는 점 하나를 잡아서 그에 대한 기울기 순으로 정렬을 할 수가 있다. 이 때 이분탐색을 통해서 O(logN)만에 점이 위와 같이 나눠진 구역들 중 어느 구역에 속해있는지 알 수 있고, 이를 이용해 바로 점이 도형의 내부에 있는지 외부에 있는지 알 수 있다.
예를 들어서 3번 반직선과 4번 반직선 사이에 점이 있다는 것을 알게 되었으면 점이 아래의 삼각형안에 있는지만 확인하면 된다.

물론 많이 쓰이지는 않는 알고리즘 이다.
'코딩 > 알고리즘 & 자료구조' 카테고리의 다른 글
| Geometry (4) - 로테이팅 캘리퍼스 (10) | 2020.03.13 |
|---|---|
| Geometry (3) - 컨벡스 헐 잡기 (그라함 알고리즘) (0) | 2020.03.08 |
| Geometry (1) - CCW & 교차 판별 (0) | 2020.03.07 |
| Segment Tree With Lazy Propagtion (0) | 2020.02.29 |
| 알고리즘 & 자료구조 복기글 (6) Segment Tree (0) | 2020.02.19 |