서론
SCC(Strongly Connected Components)를 구할 때는 크게 타잔 알고리즘과 코사라주 알고리즘을 사용한다. 그 중에서도 코사라주 알고리즘을 사용하는 편이다. 최근에 코사라주 알고리즘의 정당성에 대한 증명을 알게 되어서, 나의 블로그에는 알고리즘의 정당성에 관한 내용이 하나도 없는 것 같아서 글을 적어보려고 한다.
먼저 읽고 와야하는 글
- SCC와 코사라주 알고리즘
- DFS ordering (혹은 Euler Tour. 꼭 이 글 안 봐도 됨)
사전 준비
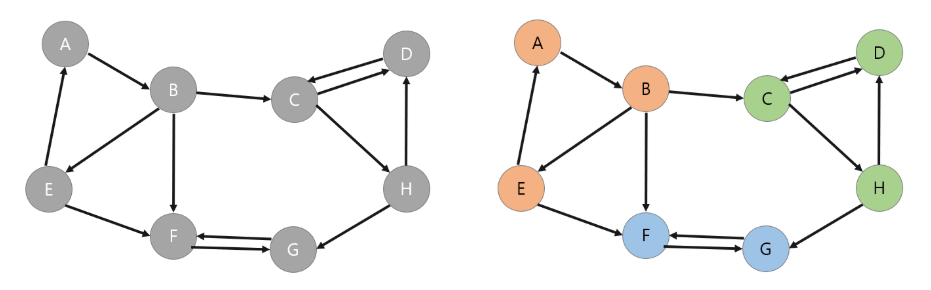
왼쪽과 같은 그래프에서 오른쪽과 같이 색깔별로 그룹을 묶었다. 이는 위의 글에서도 알 수 있듯이 코사라주 알고리즘을 통해 얻은 결과이며, 이 그룹이 SCC가 맞음을 증명할 것이다.
어떤 그룹이 SCC가 맞다는 것을 증명하기 위해서는 그 그룹내에서 임의의 노드 a와 노드 b에 대해서 a에서 b로 갈 수 있다는 것을 증명해야 하며, 그룹은 그 최대라는 것을 보여주어야 한다.
우리는 그룹을 묶을 때 스택에서 노드를 꺼내고 뒤집어진 그래프에서 그 노드에서 출발해서 갈 수 있는 곳들을 그룹으로 묶는다. 이때 그 시작한 노드를 그 그룹의 대표라고 하자. 즉 여기서는 A,C,G가 각 그룹의 대표가 된다.
정의 : ( dfs 과정에서 탐색이 완료 된다는 것은 그 노드에서 더 이상 방문할 수 있는 노드가 없게 되는 상태를 말한다.)
증명
1. 어떤 그룹 내의 노드들은 뒤집어진 그래프에서 대표노드에서 도달할 수 있는 노드들이다. 즉, 이를 다시 말하면 어떤 그룹 내의 노드들은 모두 기존 그래프에서 대표노드로 도달할 수 있다는 것이다.
2. 그룹에서 대표노드는 그룹 내의 노드중에서 가장 먼저 스택에서 꺼내진다. 즉, 맨 처음에 DFS과정에서 가장 마지막으로 탐색이 완료 된다.
3. dfs과정에서 그룹의 대표가 아닌 노드 x를 더 먼저 방문했다고 생각해보자. x에서는 대표 노드까지 도달할 수 있기 때문에 대표노드의 탐색을 완료해야만, x의 탐색을 완료할 수 있다. 이는 2에 모순이 되기 때문에 dfs 과정에서는 그룹의 대표를 가장 먼저 방문하게 된다.
4. 3번에 의해 dfs과정에서는 그룹의 대표를 가장 먼저 방문하게 된다. 이때 2번에 의해 대표노드는 그룹에서 가장 늦게 탐색이 완료 되어야 하므로, 순서는 대표노드의 방문 -> 나머지 노드의 방문과 탐색 완료 -> 대표노드의 탐색 완료 순서로 과정이 이루어져야 한다. 대표노드에서 탐색이 완료되기 전에 나머지 노드를 방문했다는 것은 대표노드에서 나머지 노드들로 갈 수 있는 경로가 존재한다는 것이다.
5. 1번에 의해서 임의의 노드에서부터 대표 노드로 가는 경로가 존재하며, 4번에 의해서 대표노드에서부터 임의의 노드로 가는 경로가 존재하기 때문에 같은 그룹내에서 임의의 두 노드에 대해서 i->대표노드->j 로 가는 경로가 존재하게 된다. 따라서 코사라주 알고리즘을 통해서 묶은 그룹은 scc를 만족한다고 할 수 있다.
'코딩 > 코딩 이모저모' 카테고리의 다른 글
| 교내 경시 대비 #1 (0) | 2020.08.07 |
|---|---|
| 6~7 월 PS 및 블로그 관련 잡다한 일지 (0) | 2020.08.01 |
| 4~5 월 PS 및 블로그 관련 잡다한 일지 (0) | 2020.06.01 |
| Semi-Game Cup 에디토리얼 (0) | 2020.05.18 |
| Semi Game cup 후기글 (문제별 후기 포함) (2) | 2020.05.18 |