'Tree에서는 Centriod를 잡고 생각하면 편하고 그래프에서는 SCC를 잡고 생각하면 편하다.' 라는 말이 있다. 사실 수준급의 그래프 문제를 많이 풀어본 것이 아니라서 별로 공감은 안되지만, SCC가 정말 좋은 테크닉이라는 것은 인정하고, 저러한 말이 나올 정도로 굉장히 유용하게 쓰일 수 있다. 이번 포스팅은 그러한 SCC에 대해서 설명하려고 한다.
SCC
scc란 무엇일까? scc는 strongly connected component로 약자를 풀어내면 해석이 되는 다른 줄임말과 다르게 바로 알 수가 없다. 보통 방향그래프에서의 scc를 말하며, scc는 아래의 두가지 조건을 만족하는 서브 그래프이다.
1. 한 scc안에 속한 임의의 어떤 한 노드 A와 다른 한 임의의 노드 B에 대해서 A에서 B로 갈 수 있는 경로가 존재한다.
2. 어떠한 scc에 속하지 않은 어떠한 노드도 scc에 추가로 들어왔을 때 1의 성질을 만족하면 안된다.
즉 내부에서 자유롭게 이동이 가능한 최대 크기의 노드 집합을 뜻한다. 이를 예시를 들어보면

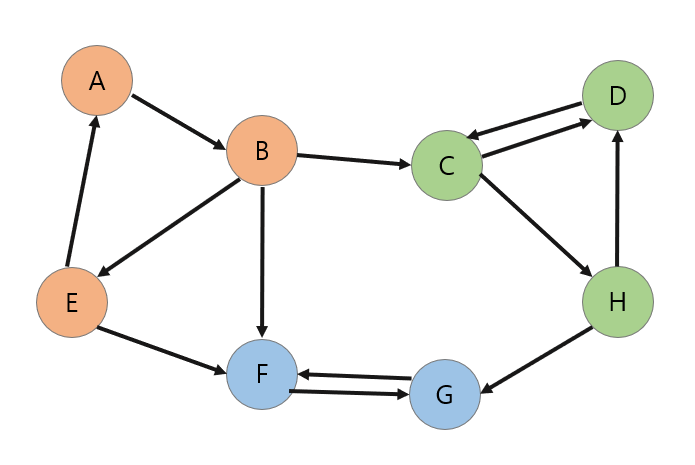
왼쪽과 같은 그래프에서 scc별로 묶으면 오른쪽의 색칠과 같이 3개의 scc로 만들어진다. 여기서 좀 더 생각해보면 (A,B,E),(C,D,H),(F,G)의 3개의 scc에서 (A,B,E) -> (C,D,H) -> (F,G)의 순서관계가 나오게 된다. 여기서 굉장히 중요한 점을 말하자면, 모든 방향그래프는 SCC들의 위상정렬로 나타낼 수 있다.
SCC 구하기
그렇다면 주어진 방향 그래프에서 SCC를 어떻게 구할 수 있을까? 보통은 잘 알려진 코사라주 알고리즘과 타잔 알고리즘의 두 가지 방법이 있지만, 이 글에서는 코사라주 알고리즘에 대해 설명하려고 한다.
코사라주 알고리즘
코사라주 알고리즘은 다음과 같은 방식으로 진행된다.
1. 아직 방문하지 않은 점 부터 dfs를 실시한다. (이를 그래프의 모든 점을 방문할 때 까지 반복한다.)
2. dfs하는 과정에서 방문이 완료된 순서대로 스택에 담는다.
3. 그래프의 모든 간선을 뒤집은 새로운 그래프를 만든다.
4. 새로운 그래프에 대해서 스택의 제일 위에서 꺼내는 순서대로 아직 방문하지 않았다면 dfs를 시작한다.
5. 4번 과정에서 어떤 한 시작점에 대해서 한 번에 방문한 모든 노드를 SCC로 묶으면 된다.


일단 1,2 번 과정을 시행하면 왼쪽과 같이 진행이 된다. A에서 시작을 하고, dfs로 모든 노드를 탐색했기 때문에 한 번의 dfs만으로도 충분하였다. 또한 dfs 과정에서 아래의 stack에 dfs를 한 순서대로 노드를 담았다.
오른쪽 그림은 기존의 그래프에서 모든 선분을 뒤집은 3번과정에 해당하는 그래프이다.


스택에서 가장 위에 있는 A를 꺼내면서 A에서 갈 수 있는 E와 B를 같이 SCC로 묶는다. 따라서 (A,B,E)의 SCC가 완성.
그 다음 스택에서 가장 위에 있는 B를 꺼내보지만, B는 이미 SCC에 속해 있기 때문에 무시한다.
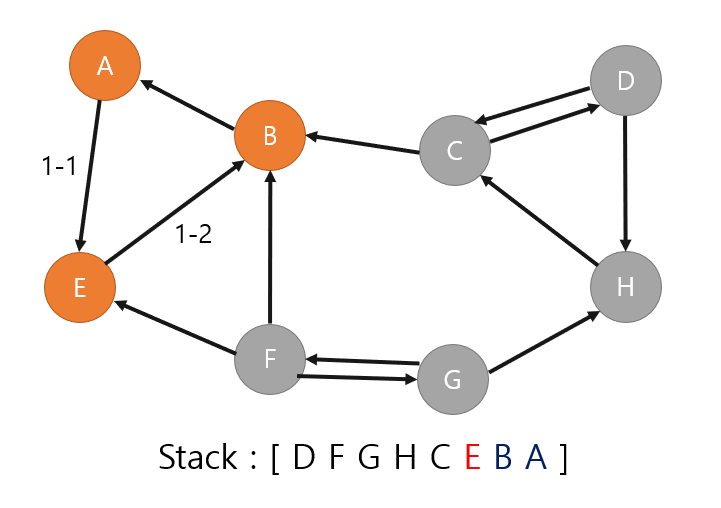
그 다음으로는 E를 꺼낼 차례이지만, E 또한 이미 방문을 한 적이 있기 때문에 넘어간다.
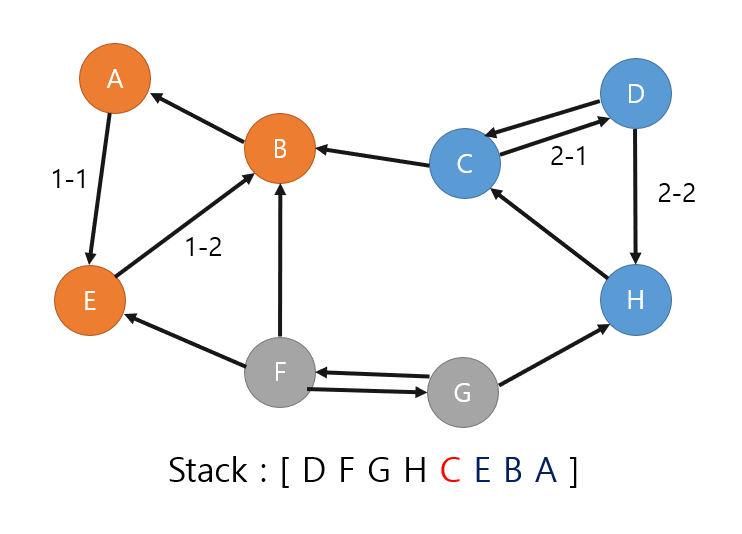
그 다음은 C를 꺼내게 되고, C에서 dfs를 통해 D와 H를 방문하였기 때문에 그 셋을 SCC로 묶는다. 따라서 (C,D,H)의 SCC가 만들어지게 된다.
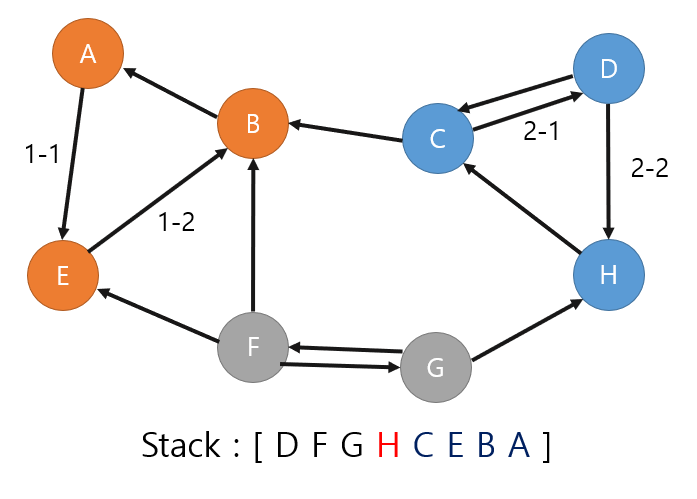

그 다음으로는 H를 꺼낼 차례이지만, H는 이미 방문을 한 적이 있기 때문에 넘어간다.
그 다음은 G를 꺼내게 되고, G에서 dfs를 통해 F를 방문하였기 때문에 그 둘을 SCC로 묶는다. 따라서 마지막으로, (F,G)의 SCC가 만들어지게 된다.
이 뒤로는 모든 노드가 SCC에 속해있으므로 계속 넘어가게 될 것이고 따라서 위와 같이 완성이 되게 된다.
여기서 한가지 더 재밌는 사실을 말해주자면 SCC가 완성되는 순서는 위상정렬의 역순이 되게 된다.
코드
아래의 코드는 BOJ 2150 SCC를 푸는 코드이다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
|
#include<bits/stdc++.h>
using namespace std;
typedef long long int ll;
typedef pair<ll,ll> pii;
#define ff first
#define ss second
#define ep emplace_back
#define eb emplace
#define pb push_back
ll arr[1010101];
vector<ll> v[101010];
vector<ll> rev[101010];
vector<ll> scc[101010];
ll vis[101010];
stack<ll> st;
ll gp;
void dfs(ll x){
vis[x]=1;
for(auto k:v[x]){
if(vis[k]) continue;
dfs(k);
}
st.push(x);
}
void dfs2(ll x){
vis[x]=1;
scc[gp].pb(x);
for(auto k:rev[x]){
if(vis[k]) continue;
dfs2(k);
}
}
bool sf(vector<ll> va,vector<ll> vb){
return va[0]<vb[0];
}
int main(){
ll i,j,k,l,m,n;
scanf("%lld %lld",&n,&m);
for(i=1;i<=m;i++){
ll a,b;
scanf("%lld %lld",&a,&b);
v[a].pb(b);
rev[b].pb(a);
}
for(i=1;i<=n;i++)
if(!vis[i])
dfs(i);
for(i=1;i<=n;i++)
vis[i]=0;
while(!st.empty()){
ll x=st.top();
st.pop();
if(vis[x]) continue;
gp++;
dfs2(x);
}
for(i=1;i<=gp;i++)
sort(scc[i].begin(), scc[i].end());
sort(scc+1,scc+1+gp,sf);
printf("%lld\n",gp);
for(i=1;i<=gp;i++){
for(auto k:scc[i]) printf("%lld ",k);
printf("-1\n");
}
}
|
코사라주 알고리즘의 증명
'코딩 > 알고리즘 & 자료구조' 카테고리의 다른 글
| Prefix Sum Technique (0) | 2020.06.17 |
|---|---|
| Segment Tree 응용 (3) - 구간 내 부분 합 최대 (금광 세그) (0) | 2020.06.07 |
| Segment Tree 응용 (2) - Inversion counting , LIS, 3-elements. (0) | 2020.05.29 |
| Segment Tree 응용 (1) - 응용의 기초, Segment Tree 활용 팁 (0) | 2020.05.28 |
| Mo's algorithm (모스 알고리즘) (0) | 2020.05.25 |