돌이 코딩하는 방

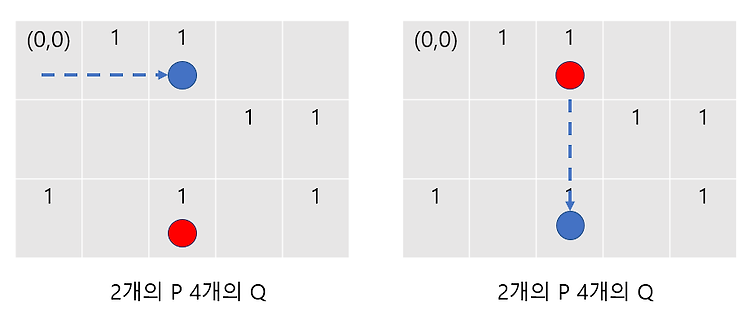
문제 링크 : https://www.acmicpc.net/problem/10067 문제 소개 길이 n의 수열을 k번 자른다. 자를 때 마다, 자른 후 양쪽 수열의 값의 각각의 합을 곱한 것만큼 점수를 얻는다. 이때 얻을 수 있는 최대 점수와 자르는 방법을 구하시오. 문제 풀이 우리는 이 문제를 최종 시점관점에서 보면서 점수에 어떤 값을 이 추가되었는지를 살펴보아야 한다. (a,b,c,d)를 (a,b),(c,d)로 잘랐다고 하자. 이러면 우리는 (a+b)*(c+d)의 점수를 얻게 된다. 이를 다른 식으로 풀어쓰면 ac+ad+bc+bd 만큼의 점수를 얻게 된다는 것이다. 이는 서로 다른 그룹에 속하는 임의의 두 값을 곱해서 더한 값이다. 결국 그전에 어떤 순서로 어떻게 잘랐건 간에, 마지막에 다른 그룹에 있..

문제 태그: https://www.acmicpc.net/problem/7578 문제 소개 2열에 걸쳐 N개의 숫자가 주어진다. 윗줄과 아랫줄에 한쌍의 같은 숫자가 선으로 연결되어있다. 교차되는 선의 쌍의 수를 구하시오. 문제 풀이 일단 같은 숫자끼리 (a,b)의 쌍을 만들어서 생각해보자. 우리는 N개의 (a,b)를 얻을 수 있으며 그중에 i,j 에 대해 $a_{i} b_{j}$ 또는 $a_{i} > b_{i}, a_{j} < b_{j}$를 만족하는 쌍의 갯수를 구하면 된다. 한 쌍의 두 값에 대해서 순서가 바뀌어있는 갯수를 세는 문제이며, 이를 흔히 inversion counting 문제라고 불린다. inversion counting 문제는 merge sort 혹은 se..

문제 태그 : https://www.acmicpc.net/problem/2357 문제 소개 N개의 숫자들이 주어지고 쿼리가 주어진다. 쿼리가 a,b가 주어지면 a번째 숫자부터 b번째 숫자 사이의 최솟값과 최댓값을 구해야 한다. 문제 풀이 지금은 N개의 숫자들이 바뀌지는 않지만, 아무튼 구간의 최댓값과 구간의 최솟값은 Segment Tree를 사용함으로써 한 번 구하는 데 $O(lgN)$에 구할 수 있음이 잘 알려져 있다. 구간합을 구할 때 구하고자 하는 구간에 포함되어지지 않는 노드는 0을 반환한다. 항등원이기 때문이다. 같은 이유로 최솟값 세그트리에서는 항등원인 inf를 반환해야 하고, 최댓값연산에서는 항등원이 -inf이므로 구간이 포함되어지지 않으면 -inf를 반환해야 한다. 코드 1 2 3 4 5 ..

문제 링크 : https://www.acmicpc.net/problem/1226 문제 소개 어떤 당이 빠져도 합이 과반수가 안되는 집합을 깔끔한 연합이라고 한다. 가장 큰 크기의 깔끔한 연합을 구하여라. 문제 풀이 가장 큰 크기의 깔끔한 연합을 구하는 것이 아니라 관점을 바꾸어서 크기가 K인 깔끔한 연합이 존재하는 지에 대해서 구해도 된다. 모든 값에 대해서 다 가능성을 구해주면 된다. 일단 기본적으로 몇 개의 값의 합이 K가 되어야 한다. 합이 K가 되는 여러가지 방법중 깔끔한 연합이 될 확률이 가장 높은 것은 것은 연합내의 가장 작은 값이 커야 한다는 것이다. 가장 작은 값만 빼더라도 과반수가 안되면 깔끔한 연합이라고 할 수 있고, 그러기 위해서는 연합내 가장 작은 값이 커야한다. 따라서 N개의 숫자..

문제 태그 : https://www.acmicpc.net/problem/2472 정말 좋은 문제라고 생각한다. 여러가지 테크닉을 같이 써야 문제를 해결할 수 있다. 그런데 최근에 재채점을 당해 틀려서 다시 푼 김에 글을 작성하였다. 문제 소개 그래프가 주어지고 3개의 출발 지점이 주어진다. 만약 지점 A와 B가 존재해서 출발지점 3곳에 대해서 모두 B가 A보다 출발 지점까지의 거리가 짧으면 A에는 매장을 설치할 수 없다. 각 지점에 대해서 질의를 던지면 그 지점에 매장을 설치할 수 있는지 대답을 해야한다. 문제 풀이 일단 그래프 상에서 어떠한 한 노드를 중심으로 다른 모든 점까지의 거리를 각각 구하는 것은 다익스트라를 3번 돌리는 것으로 쉽게 처리해 줄 수가 있다. 다르게 말하면 우리는 모든 노드에 대해..

문제 태그 : https://www.acmicpc.net/problem/11001 문제 소개 각 날 별로 넣을 때의 가치와 꺼낼 때의 온도가 주어진다. 어떤 김치의 맛은 (숙성 시간)*(김치를 꺼낼 때의 온도)+(김치를 넣은 날 가치)로 정의된다. 만들 수 있는 가장 맛있는 김치의 맛을 구하여라. 문제 풀이 이 문제를 봤을 때는 이 문제가 DnC Optimization을 쓰는 문제인지 모르고 봤다. (DnC Optimization에 대한 설명글) 그리고 풀이를 들었기 때문에 상세한 의식의 흐름과정은 설명할 수가 없다. 그대신 식을 전개해 나가면서 왜 DnC 적용이 되는지를 살펴보려고 한다. 넣은 날의 가치를 $V_i$라고 하고, 꺼낼 때의 온도는 $T_i$라고 하자. 나는 j일때 넣은 김치가 제일 맛있을..

문제 태그 : https://www.acmicpc.net/problem/3998 문제 소개 N개의 질량조건이 주어진다. 이 중 가장 큰 값과 단백질의 전체 질량이 똑같은 단백질 구조 중 주어진 질량조건에 단백질의 prefix 질량과 suffix 질량이 가장 많이 포함되어있는 단백질 구조를 출력하시오. 예제) 353.16992는 가장 큰 값으로 단백질이 P하나와 Q두개로 이루어져 있다는 것을 알려준다. 이때 구조를 PQQ또는 QQP로 배치하게 되면 P=97.05276 Q=128.05858 PQ=225.11134 PQQ=353.16992 4개로 가장 많은 질량조건을 만족시킬 수 있다. 문제 풀이 일단 몇 가지 관찰을 하는 것이 중요하다. 정말 단순하고 간단한 것 일수 있지만, 하나하나가 정말 강력하게 작용하..

문제 태그 : https://www.acmicpc.net/problem/13409 ※ 내가 관찰로 푼 문제들 중 하나이다. 따라서 갑자기 생각난 아이디어와 노가다, 말도 안되는 관찰들로 풀이가 이루어 질 예정이다. ※ Blackking과 함께 풀었다. 문제 소개 N개의 상자 그룹이 있다. 각 상자그룹은 A박스와 B박스가 쌓여있는 형태이다. 이 중 몇 그룹을 사용해서 게임을 진행할 것이다. 돌아가면서 A는 A박스와 그 위에 쌓인 박스 모두를 제거하고, B는 B박스와 그 위에 쌓인 모든 박스를 제거한다. 이렇게 진행하며 더이상 할 행동이 없는 사람이 지게 된다. 이때 공정한 게임이 될 수 있는 최대 박스의 갯수를 구하시오. (단, 공정한 게임은 먼저 하는 사람에 따라 승패가 바뀌는 게임이다.) 사고의 흐름 ..

문제 태그 : https://www.acmicpc.net/problem/15134 ※ 내가 관찰로 푼 문제들 중 하나이다. 따라서 갑자기 생각난 아이디어와 노가다, 말도 안되는 관찰들로 풀이가 이루어 질 예정이다. ※ 2018 NEERC가 끝난 후 LOTUS와 함께 풀었다. 문제 소개 테스트 케이스 별로 a,b,c,d 숫자 4개가 주어진다. 총 구슬의 갯수 $n=2^a+2^b+2^c+2^d$이다. 이때 우리는 n개의 구슬인 1묶음을 1개의 구슬씩 n개의 그룹으로 나누어야 한다. 이때 한 번의 행동으로 다음과 같은 작업을 할 수 있다. - (A,B,C) 그룹의 크기가 A인 모든 그룹을 각각 크기가 B인 그룹과 C인 그룹으로 나눈다. (이때 $A=B+C$) 이때 그룹의 최대 크기가 1이 될때까지 걸리는 행동..

최근에 어려운 문제들을 도전해 보면서 느꼈는데 난 관찰에 제일 강한 것 같다. 그냥 문제에서 얻을 수 있는 단서를 관찰하는 능력도 떨어지지는 않지만, 내가 직접 손으로 예제를 만들고 풀어보면서 답을 찾은 경우가 굉장히 많다. 직접 혼자 게임을 진행하며 승리 방법과 조건을 찾는다던가, 작은 모든 경우에 대해 다 해보면서 방향성이나 중요한 사실들을 관찰하는 경우가 꽤 있었다. 툭툭 던진 말이 중요했던 경우도 꽤 많았고, 애초에 이런 것이 좋아서 시작하게 된 PS이다. 사실 이러한 부분을 제외하면 stonejjun이라는 코더가 그렇게 특별한지도 모르겠고, 엄청 뛰어난지도 모르겠다. 개인대회에 그렇게 강점이 있는지 모르겠다. 스페셜리스트 같은 느낌인것 같기도 하다. 이상한 말들은 그만하고, 이 글의 진짜 목적은..