LCA란?
LCA는 Lowest Common Ancestor의 약자로 해석하면, 최소 공통 조상(가장 낮은 공통 조상)이라는 뜻을 가지고 있다. '조상'이기 때문에 트리에서 사용하며, 다양한 특징을 가지고 있어 트리 문제를 해결할때 기초로 잘 사용되어진다.
트리에서는 조상이 존재한다. 어떤 노드의 부모, 부모의 부모, 부모의 부모의 부모해서 루트까지의 모든 노드를 조상노드라고 하며, 공통 조상은 2개의 노드들에 대하여 어떤 노드가 그 두 노드의 공통적으로 조상일때를 말한다. 그러한 공통 조상들 중에서 가장 낮은 (깊이가 깊은, 처음 만나는) 공통조상이 최소 공통 조상 즉 LCA가 된다.
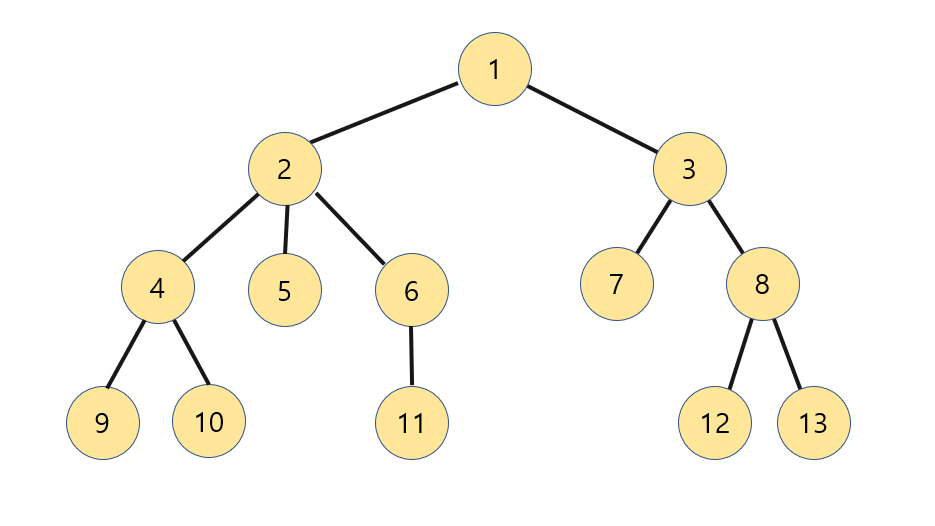
위와 같은 트리가 있다고 할 때
LCA(9,10)=4, LCA(9,11)=2, LCA(5,9)=2, LCA(12,13)=8, LCA(9,13)=1, LCA(9,7)=1, LCA(1,9)=1, LCA(2,11)=2
등등 어떤 두 노드에 대해서라도 LCA가 나오게 됩니다.
LCA를 구하는 방법
두 노드의 LCA를 구하는 과정은 보통 두 개의 단계로 진행된다.
1. 두 노드의 깊이 맞추기
2. 두 노드가 같아질 때 까지 올리기.
맨 처음에 dfs등을 통해서 모든 노드의 깊이를 알아 낸 후, 1번 과정에서 더 깊은 노드를 올려줌으로 써 깊이를 맞춰준다.
그 사이에 LCA가 있지는 않기 때문에 문제가 없으며 이 과정을 통해 두 노드를 똑같은 만큼만 올려도 LCA에 이룰 수 있게 만들어주는, 일종의 전처리 같은 과정이다.
2번과정에서는 말그대로 두 노드를 올리면서 같아지는 시점에 딱 멈추면 된다. 예를 들어 위의 트리에서 시작부터 4,4 였으면 바로 멈추고 4라는 결과가 나왔을 것이며, 5와 8이었다면 (5,8)->(2,3)->(1,1)->답: 1이 나왔을 것이다.
$O(N)$ 방법
1번과 2번 과정에서 노드를 올리는 것을 한 칸씩 올리면 된다. 최악의 경우 ㅅ모양의 트리나 일자형 트리에서 양 끝에 배치 되어있다면 LCA 하나를 구하는데 $O(N)$의 시간복잡도가 걸릴 것이다.
$O(lgN)$ 방법
하지만 LCA 한 번을 구하는 과정을 $O(lgN)$에 할 수 있다. 다만 전처리로 $(NlgN)$이 필요하게 된다.
스파스 테이블(모르겠다면 그냥 배열이라고 생각하자) par[i][j]에 i의 2^j번째 조상을 저장해 놓는다. i의 $2^j$번째 조상은 i의 $2^{j-1}$번째 조상의 $2^{j-i}$번째 조상으로도 말할 수 있다. 이를 배열에서의 식으로 표현하면
par[i][j]=par[par[i][j-1][j-1]]로 표현할 수 있을 것이다. 이를 이용하여 미리 거듭제곱 형식의 조상 배열을 완성할 수 있다.
이를 이용하여 노드들을 올릴 때 비트에 따라 올릴 수 있다. 예를 들어 1번과정에서 노드 a를 42단계 올리고 싶을 때, 이를 42번 반복하는 것이 아니라, 32단계+8단계+2단계의 3번의 과정만에 a의 위치를 올릴 수 있다.
2번과정은 몇 번 올릴지 모르기 때문에 가장 큰 단위부터 시작한다. 두 노드의 $2^20$번째 조상을 확인하고, 같으면 올리지 않고, 다르면 올린다. $2^19$번째 조상을 확인하고... $2^18$번째 조상을 확인하고... 이를 반복하면 된다. 이 과정은 만약 내가 k만큼 올려야 한다면 그 전까지는 올리지 못하다가 k의 가장 큰 비트값만큼 올리고 그 값을 빼는 과정을 반복한다는 것이다.
예를 들어서 19단계를 올리는 것이 LCA였다면 $2^20$단계만큼 올릴 때부터 $2^5=32$단계를 올릴 때까지는 두 값이 같을 것이다. $2^4$단계를 올리면 둘이 다르기 때문에 올리면 3단계만큼만 더 올리면 되고, 위의 과정을 반복하게 된다.
코드
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
void dfs(ll x,ll d){
vis[x]=1;
dep[x]=d;
for(auto n:v[x]){
if(vis[n.ss]) continue;
par[n.ss][0]=x;
dfs(n.ss,d+1);
}
}
void f(){
ll i,j;
for(j=1;j<21;j++)
for(i=1;i<=n;i++)
par[i][j]=par[par[i][j-1]][j-1];
}
ll lca(ll x,ll y){
if(dep[x]>dep[y]) swap(x,y);
for(int i=20 ;i>=0;i--){
if(dep[y]-dep[x]>=(1<<i)) y=par[y][i];
}
if(x==y) return x;
for(int i=20;i>=0;i--){
if(par[x][i]!=par[y][i]){
x=par[x][i];
y=par[y][i];
}
}
return par[x][0];
}
Colored by Color Scripter
|
코드 설명
dfs 함수로 노드의 깊이, 부모 노드를 구해준다.
f함수에서 dfs의 결과를 이용해 조상 배열의 나머지 부분을 모두 채워준다.
lca를 돌릴 때 y를 항상 더 깊게 바꿔주고 for문을 이용해 깊이를 맞춰준 후, 둘이 같으면 바로 반환하고 아니면, 일련의 과정을 통해 lca 바로 밑 노드를 구해준 후 그의 부모를 반환한다.
추천 문제
'코딩 > 알고리즘 & 자료구조' 카테고리의 다른 글
| Segment Tree 응용 (1) - 응용의 기초, Segment Tree 활용 팁 (0) | 2020.05.28 |
|---|---|
| Mo's algorithm (모스 알고리즘) (0) | 2020.05.25 |
| 파라매트릭 서치(Parametric Search) (0) | 2020.04.10 |
| Techniques In DP (3) - DnC Optimization (0) | 2020.04.08 |
| Techniques In DP (2) - CHT (Convex Hull Trick) (1) | 2020.03.27 |